Bone has a hierarchical structure with outstanding mechanical properties: it combines the high stiffness of the mineral phase (mainly hydroxyapatite) and the high toughness of the organic phase (mainly collagen). Because of its complicated structure and extraordinary characteristics, bone has been intensively studied at different length scales. One of the powerful techniques to unravel the relationship between structure and property is finite element (FE) simulation. FE simulation has been proven useful in bone mechanics: it has been applied to predict the elastic, plastic, viscoelastic and damage properties of bone. However, most of the FE simuation has been performed on the higher hierarchical structural levels of bone, which are at the macroscopic or microscopic scale. In our group, Alix and Anjali are studying mechanical properties of bone at collagen fibril level by using synchrotron X-ray diffraction at Argonne National Laboratory. Their experimental measurement provides excellent information on bone mechanics at nanoscale. My research here is to create FE models which present bone structure at collagen fibril level and simulate their mechanical responses to reproduce and explain the experimental strain evolution in different phases of bone, and therefore improve the understanding of structure-property relationship of bone at this level.
In the model the bone is divided into two phases: mineral phase and the hydrated collagen phase, which is the combination of collagen and water. Based on the nanoscale structure of mineralized collagen fibril, several different geometrical models have been made to represent the different degrees of structural simplification (Figure. 1). The simulations on the models are performed in the exact same loading conditions as during the experimental measurements. The strains in the hydroxyapatite crystals and in the fibril can be directly deduced from the model. The high similarity between the modeling results and experimental data verifies the credibility of the simulation work, which gives insight into the detailed load transfers between these phases. For example, Figure 2 shows the comparison between simulation and experimental results of the elastic properties of bone at collagen fibril level.
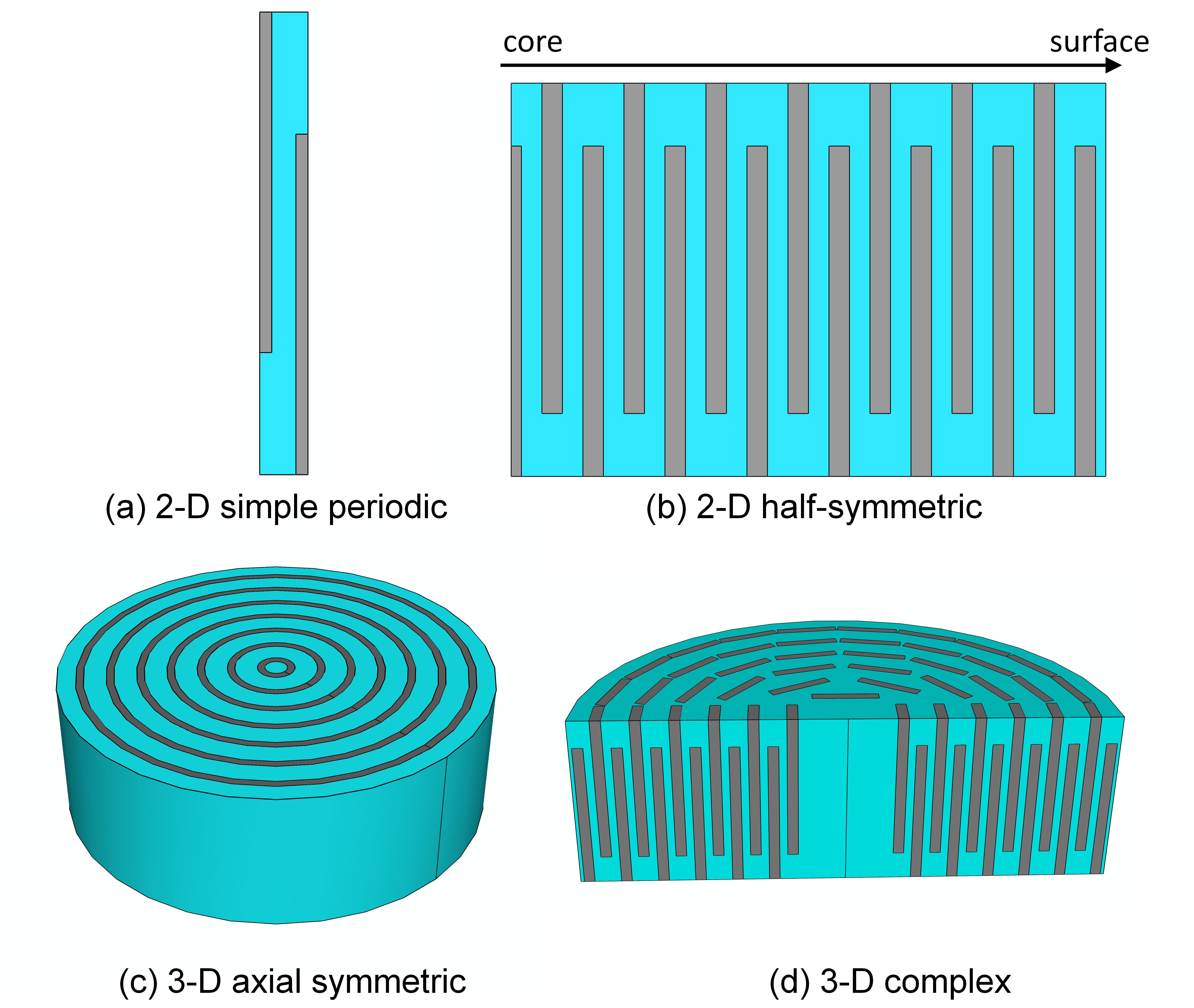
FIGURE 1: Four geometrical models used to approximate the mineralized collagen fibril geometry (mineral phases are shown in gray color). |
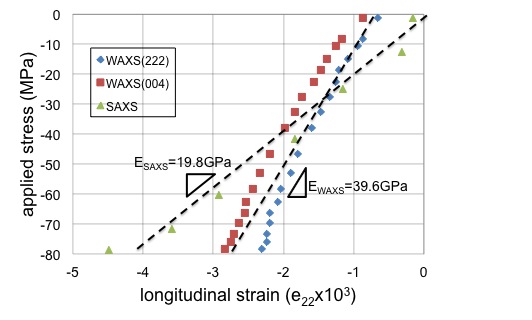
FIGURE 2: Comparison between the average strains measured in mineral phase (from 00.4 (in red squares) and 22.2 (in blue diamonds) reflections, WAXS) and in fibril phase (in green triangles, D-period, SAXS) as a function of applied stress on a sample from a canine fibula and simulation results in black dashed lines. The slopes are the apparent moduli of each phase. |
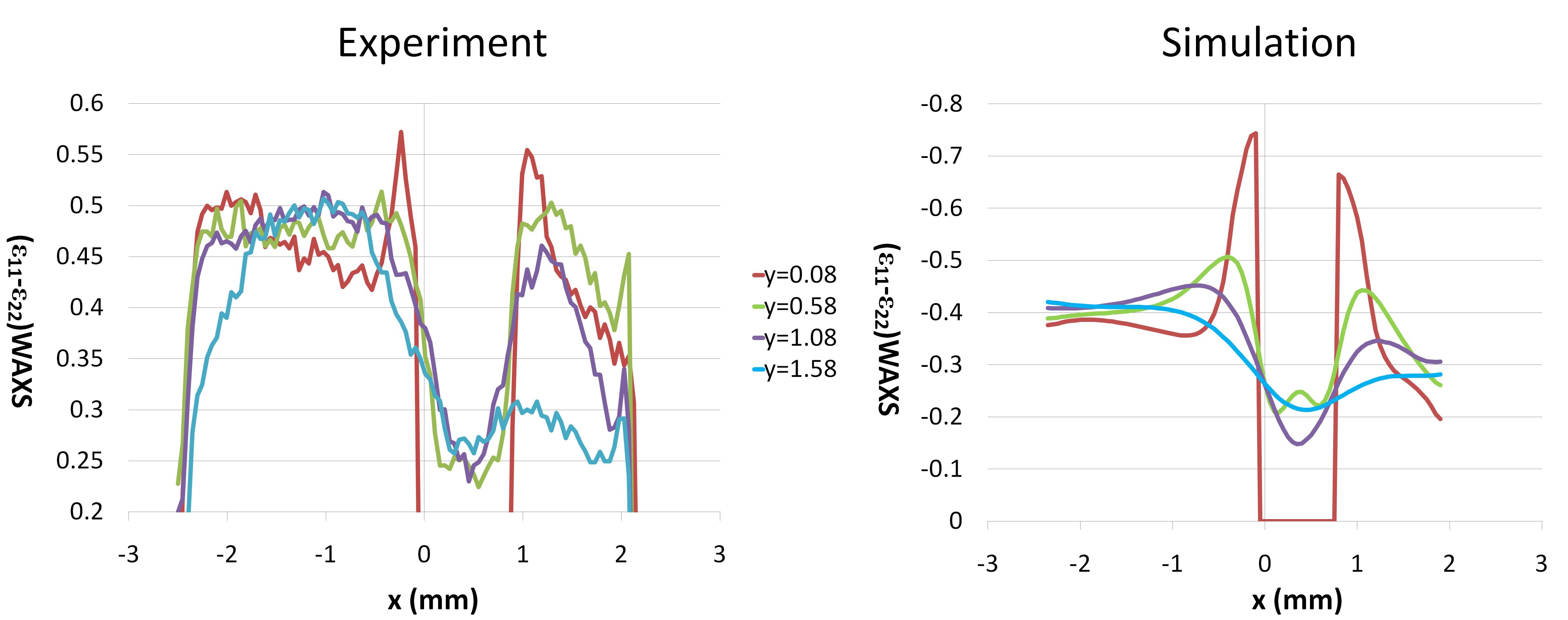
FIGURE 3: The distribution of deviatoric strains in mineral phase in the bulk bone sample. Left: Experimental data from synchrotron X-ray diffraction. Right: Simulation results from FE modeling.
The above model created at nanoscale level is further connected to the macroscopic models to understand the distribution of collagen fibril level strains at macroscopic scale. In the first step, the distribution of macroscopic strains is calculated by FE simulation, then in the second step, these macroscopic strains are applied to the nanoscale level FE model as input information, therefore the distribution of nanoscale strains of different phases can be deduced. Figure 3 shows an example of the mapping of strains in the hydroxyapatite crystals on bulk sample.
Related Publications
- F. Yuan, S. R. Stock, D. R. Haeffner, J. D. Almer, D. C. Dunand, L. C. Brinson, A new model to simulate the elastic properties of mineralized collagen fibril, Biomechanics and Modeling in Mechanobiology, in press, doi: 10.1007/s10237-010-0229-3
- S. R. Stock, F. Yuan, L. C. Brinson, J. D. Almer, Internal strain gradients quantified in bone under load using high-energy X-ray scattering, Journal of Biomechanics 44, 291 (2011)
Financial Support
This research is financially supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Contract No. DE-AC02-06CH11357

